精选金句
学会开车和了解内燃机的工作原理是两种不同的追求。驱动车辆更为实用,但掀开引擎盖观察内部机制却有种深层满足感。 这台机器暴露了函数中特定的指数部分。它暴露了指数s的值以及相应的系数。 当你对指数函数求导时,其效果完全等同于乘以一个系数s。这就是为什么拉普拉斯变换能将微分方程转变为代数。 解析延拓就像是在复平面上,原本看似无理的区域却隐藏着能反映函数核心特征的有用信息。 变换后的函数极点,实际上就是原函数中潜伏的指数组成部分的真实写照。
内容概要
- 引入:为什么我们要掀开“拉普拉斯变换”的引擎盖?
对于学习微分方程的学生来说,拉普拉斯变换(Laplace Transform)往往像是一个黑盒工具:你输入一个复杂的导数方程,通过查表寻找对应的代数式,解出结果后再转回去。虽然这在实践中非常有效,但如果不理解它为何有效,学生往往会沦为公式的奴隶。本文旨在通过可视化直觉,向读者展示这台数学机器内部的精密结构。拉普拉斯变换不仅仅是一个技巧,它是一种看待函数和物理系统的全新视角。
2. 基石:重新定义指数函数与s平面
要理解拉普拉斯变换,首先必须对指数函数 $e^{st}$ 有深刻的理解。在这里,$s$ 不仅仅是一个实数,而是一个复数($s = \sigma + i\omega$)。
- 虚部(Imaginary part):决定了函数在复平面上的旋转频率。如果 $s$ 有虚部,输出会随时间推移而旋转。
- 实部(Real part):决定了幅度的增长或衰减。负实部意味着幅度趋向于零(衰减),正实部意味着指数级增长。
工程师通过“s平面”来可视化所有可能的 $s$ 值。在这个平面上,每一个点都代表了一种特有的行为模型(衰减、振荡、增长或其组合)。
3. 核心机制:指数分解与代数化
为什么数学家对指数函数情有独钟?因为指数函数的导数依然是它本身,只是多出了一个系数 $s$。这一特性是拉普拉斯变换的灵魂:它能将微积分中的微分操作替换为代数中的乘法。这使得求解复杂的动力学方程(如阻尼振子)变得像解一元二次方程一样简单。
许多物理函数(如余弦波 $\cos(t)$)都可以拆解为指数函数的组合。例如,余弦波可以视为两个反向旋转的虚数指数向量的平均值。拉普拉斯变换的任务就是“探测”并揭示一个函数中究竟潜伏着哪些指数成分。
4. 深入积分内部:可视化“极点”的诞生
拉普拉斯变换的标准定义是:$F(s) = \int_0^{\infty} f(t) e^{-st} dt$。
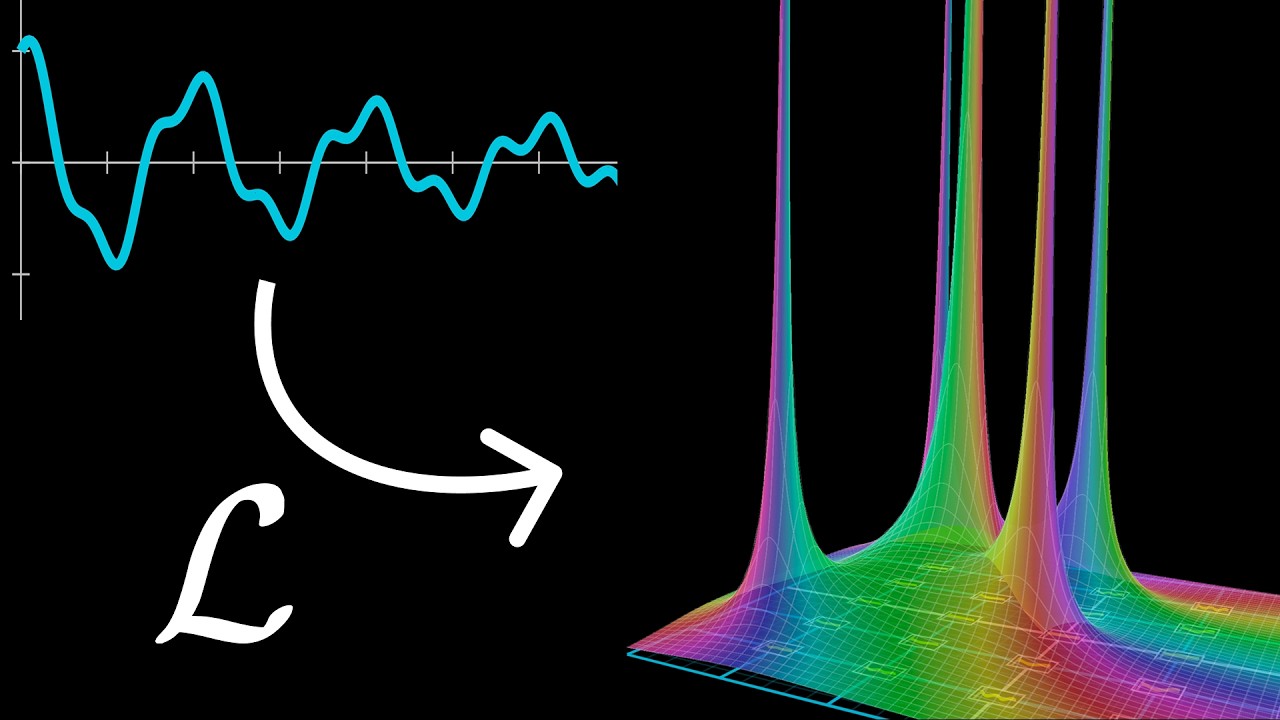
想象你正在s平面上移动 $s$ 的值,就像是在探测某种频率。当 $s$ 的值与函数 $f(t)$ 内部蕴含的规律相匹配时,积分内部的表达式就会变得“单调”或变成常数。此时,由于对常数进行从 0 到无穷大的积分会导致数值爆炸,转换后的函数 $F(s)$ 就会在那个特定的 $s$ 点位置产生一个“尖峰”或“极点”(Pole)。
例如,如果 $f(t) = 1$(常数函数),其经过拉普拉斯变换后在 $s=0$ 处有一个极点,结果为 $1/s$。这意味着简单的常数可以被视为频率和衰减率均为 0 的指数函数。
5. 向量求和视角与解析延拓
在积分的过程中,我们可以将 $e^{-st}$ 视为一个在复平面上不断旋转和缩小的向量。积分本质上是找这些向量在一段时间内的“平均重心”并进行加和。通过可视化这种螺旋路径,我们可以观察到:
- 当 $s$ 远离极点时,向量快速旋转并相互抵消,导致积分值很小。
- 当 $s$ 靠近极点时,路径变得不再抵消,而是向外延伸,导致积分值激增。
一个关键的数学难题是:当 $s$ 的实部为负时,积分通常会发散(趋于无穷),这使得左半个s平面理论上是无定义的。然而,通过“解析延拓”,数学家找到了一种唯一的方法来扩展这些函数。这就像是原本断掉的曲线,根据其现有的斜率和变化规律,只能有一种最合理的补全方式。延拓后的函数暴露了所有的极点,无论它们位于平面的哪个角落。
6. 实战演练:以受迫谐振子为例
以一个受外部驱动力影响的弹簧振子为例。其解通常包含四个指数项:两项对应系统的自然频率(自然振荡与衰减),两项对应外部驱动力的频率。如果你对该系统进行拉普拉斯变换,你会得到一个拥有四个极点的函数。通过解析这些极点的位置,我们可以直接断定系统的稳定性、共振频率以及它随时间衰减的速度,而无需手动去解每一个繁琐的微分步骤。
7. 总结:从傅里叶到拉普拉斯的泛化
如果说傅里叶变换是专注于“纯圆周运动”(虚数轴上的 $s$)的工具,那么拉普拉斯变换就是它的泛化版本,它不仅探测振荡,还探测增长和衰减。它为我们提供了一种通用的语言,将动态变化的物理世界映射到一个静止的、由极点构成的代数景观中。掌握了极点的分布,你就掌握了系统运行的终极蓝图。